高斯溅射:重新定义 3D 场景渲染的突破性技术
在 3D 场景表示与新视角渲染领域,一项名为高斯溅射的技术正引发广泛关注。它摆脱了神经网络的束缚,凭借独特的 3D 高斯分布表示方式,实现了实时渲染的惊人性能,为 3D 视觉领域带来了全新的思路。
技术革新:为何高斯溅射脱颖而出
当 3D 渲染技术还在为神经网络模型的复杂计算所困扰时,高斯溅射的出现打破了这一僵局。2023 年,《3D Gaussian Splatting for Real-Time Radiance Field Rendering》一文提出的这一方法,以其非神经性、高渲染速度和高可解释性,迅速成为该领域的焦点。
与神经辐射场(NeRF)等依赖神经网络的模型不同,高斯溅射完全不涉及任何神经网络组件。一个 3D 场景在它的表示下,就是空间中一组明确的点 —— 更准确地说,是数百万个 3D 高斯分布。这种简单直接的表示方式,不仅让其具有极高的可解释性,也为实时渲染奠定了基础。
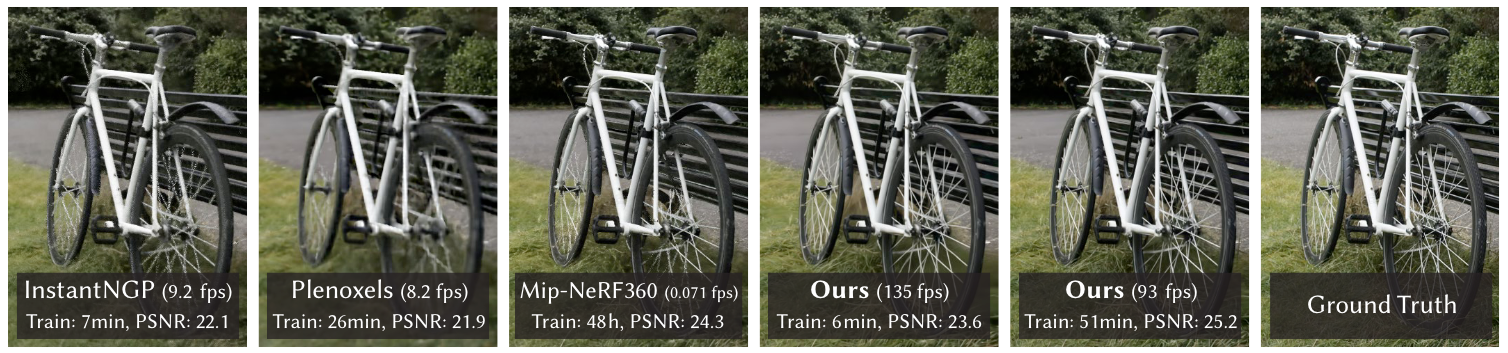
从性能数据来看,高斯溅射的优势显而易见。在相同场景下,它的渲染速度远超 Plenoxels、Mip-NeRF360 等方法,甚至能达到每秒上百帧的水平,而训练时间却大大缩短,通常只需几分钟到几十分钟。这种速度与精度的平衡,使其在众多 3D 表示方法中独树一帜。
值得一提的是,高斯溅射的理念并非凭空出现,它源于 2001 年的 “表面溅射” 技术,这也印证了经典计算机视觉方法在当代仍能焕发出强大的生命力。在人工智能模型参数规模不断刷新纪录的当下,这种回归简单、依托明确数学模型的方法,无疑为 3D 视觉研究提供了一条新的路径。
3D场景的核心表达:从点到高斯分布
高斯溅射对 3D 世界的表示方式,是其实现高性能的基础。不同于传统的点云或体素表示,它采用的是数百万个 3D 高斯分布的集合,每个分布都拥有独特的参数,这些参数通过对具体场景的拟合而来,目的是让渲染结果与真实图像高度吻合。
每个 3D 高斯分布的核心参数包括:
- 均值 μ:即空间位置坐标(x, y, z),决定了高斯分布在 3D 空间中的中心位置;
- 协方差 Σ:描述高斯分布的形状,通过特征分解为缩放矩阵和旋转矩阵,实现各向异性的椭球体表示;
- 不透明度 σ(α):控制高斯分布对最终渲染结果的贡献程度,经 sigmoid 函数映射到 [0,1] 区间;
- 颜色参数:既可以是简单的 RGB 三色值,也可以是基于球谐函数的系数,用于表示视角相关的颜色特性。
协方差矩阵的设计是其中的关键。通过将协方差矩阵分解为缩放矩阵 S 和旋转矩阵 R,即 Σ = RSSᵀRᵀ,既保证了矩阵的半正定特性,又简化了参数优化过程。缩放矩阵 S 包含 3 个参数,控制椭球体在三个方向上的拉伸程度;旋转矩阵 R 由四元数表示,决定了椭球体的空间朝向。这种设计使得每个高斯分布能够灵活地适应场景中的各种几何结构,无论是平坦的表面还是复杂的细节。
3D 高斯分布对空间中点的影响遵循多元正态分布的规律,其公式为 fᵢ(p) = σ(αᵢ) exp (-1/2 (p - μᵢ)Σᵢ⁻¹(p - μᵢ))。这意味着每个高斯分布在空间中都有无限的影响范围,但影响力随距离的增加而迅速衰减,这种特性使得它能够有效地表示局部区域的几何和外观信息。
图像渲染的奥秘:从3D到2D的映射
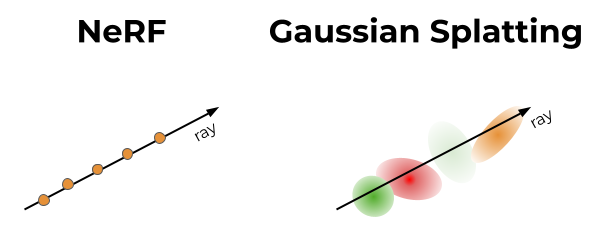
高斯溅射之所以能实现实时渲染,其独特的图像形成模型和渲染流程功不可没。与 NeRF 的体积渲染公式相比,两者在本质上有相似之处,但在实现细节上的差异导致了性能的巨大悬殊。
NeRF 通过对射线沿线的样本进行积分来计算像素颜色,而高斯溅射则是基于 3D 高斯分布投影到 2D 平面后的贡献进行聚合。具体来说,像素 p 的颜色 C (p) 由一系列投影后的 2D 高斯分布的贡献加权求和得到,权重考虑了前面高斯分布的透射率影响,公式为 C (p) = Σᵢ∈N cᵢfᵢ²ᴰ(p) × [∏ⱼ⁼¹ⁱ⁻¹(1 - fⱼ²ᴰ(p))]。
将 3D 高斯分布投影到 2D 平面是渲染过程的关键步骤。首先,通过相机的内参矩阵 K 和外参矩阵 W,将 3D 高斯分布的均值 μ 投影到像平面,得到 2D 均值 μ²ᴰ = K (Wμ) / (Wμ)_z。然后,根据投影的雅可比矩阵 J 计算 2D 协方差 Σ²ᴰ = JWΣWᵀJᵀ。这一过程完全可微分,确保了后续优化过程的可行性。
为了提高渲染效率,高斯溅射采用了基于瓦片的排序策略。将图像划分为 16×16 的像素瓦片,每个 3D 高斯分布根据其投影范围归属到相应的瓦片。在渲染时,每个瓦片内的高斯分布按深度排序,使得像素颜色的计算只需考虑所属瓦片中的相关高斯分布,大大减少了计算量。这种策略结合定制的 CUDA 内核,使得渲染速度达到实时级别成为可能。
精益求精:优化过程的关键环节
要让数百万个 3D 高斯分布准确地表示 3D 场景,优化过程至关重要。这一过程包括初始化、随机梯度下降(SGD)优化和自适应密集化三个关键环节。
初始化阶段通常利用运动恢复结构(SfM)生成的稀疏点云作为起点,将每个点初始化为各向同性的高斯分布,其半径根据相邻点的平均距离确定,以保证对场景的初步覆盖。如果没有 SfM 点云,也可以采用随机初始化,但可能会影响最终的重建质量。
在 SGD 优化阶段,通过最小化渲染结果与真实图像之间的 L1 损失和 D-SSIM 损失,不断调整高斯分布的参数。损失函数的梯度引导参数向更优的方向更新,使得渲染结果逐渐接近真实场景。
自适应密集化是提高场景表示精度的重要手段。在训练过程中,每隔一定的迭代次数(如 100 次),对那些梯度较大的高斯分布进行分裂,以增加对细节区域的表示能力;同时,移除不透明度极低的高斯分布,减少冗余。这种动态调整机制使得高斯分布能够在需要的地方密集分布,在不重要的地方稀疏存在,实现了效率与精度的平衡。
视角相关颜色:球谐函数的妙用
为了表示物体表面因视角变化而产生的颜色差异(如高光、反射等非朗伯效应),高斯溅射引入了球谐函数(SH)来描述视角相关的颜色特性。
球谐函数是定义在球面上的正交函数集,通过选择不同的阶数ℓ和次数 m,可以得到一系列函数。在高斯溅射中,通常选择ℓmax=2 的球谐函数,每个颜色通道(R、G、B)由 9 个系数表示,通过这些系数的线性组合,可以计算出不同视角下的颜色值。
具体来说,对于每个 3D 高斯分布,学习 9 个球谐函数系数,当从某个方向观察时,根据该方向的球坐标计算相应的球谐函数值,与系数加权求和后经 sigmoid 函数映射,得到该视角下的颜色。这种方法能够有效地捕捉各种视角相关的视觉效果,显著提升渲染质量。
挑战与局限
尽管高斯溅射取得了显著的成功,但它也存在一些局限性。首先,其优化过程依赖大量的启发式正则化方法,以防止高斯分布出现过大、过长或冗余等问题。其次,作为一种离散表示方法,它缺乏 NeRF 等连续表示方法的隐式插值能力,在处理未充分观测的区域时可能出现伪影。
此外,存储场景所需的高斯分布参数文件体积较大,对于资源受限的设备来说可能是一个挑战。同时,在动态场景的表示上,高斯溅射的表现还有待提升,尽管已有相关研究(如 Dynamic 3D Gaussians)进行探索,但仍面临不少困难。
参考文献
- Kerbl, B., Kopanas, G., Leimkühler, T., & Drettakis, G. (2023). 3D Gaussian Splatting for Real-Time Radiance Field Rendering. SIGGRAPH 2023.
- Mildenhall, B., et al. (2020). NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. ECCV 2020.
- Zwicker, M., et al. (2001). Surface Splatting. SIGGRAPH 2001.
- Luiten, J., et al. (2023). Dynamic 3D Gaussians: Tracking by Persistent Dynamic View Synthesis. International Conference on 3D Vision.
- Yu, A., et al. (2023). Plenoxels: Radiance Fields without Neural Networks. CVPR 2022.
